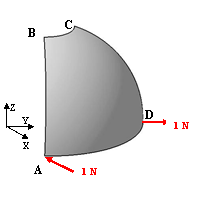
Hemispherical Shell under Concentrated Loads

The purpose of this test is to check shell elements with double curvature. You will use 2D meshes.

Reference:

MAC NEAL R.H., HARDER R.L., A Proposed Standard Set of Problems to Test Finite Element Accuracy, Finite Element Design, Vol.1, pp.3-20, 1985.
 

Specifications

Geometry Specifications

Radius:
R = 10 m
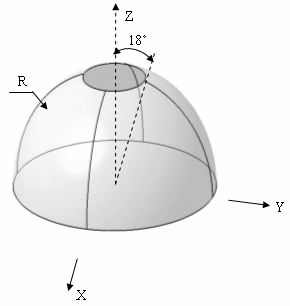Angle:
θ = 18 deg

Thickness:
th=0.04 m

Equation:
x2 + y2 + z2 = 100  

For symmetry reasons, only a quarter of the hemisphere is modeled. The given results are the same for a quarter or for the whole hemisphere.

Analysis Specifications

Young Modulus (material):
E = 68.25 MPa

 

Poisson's Ratio (material):
ν= 0.3

Mesh Specifications:

  • Imposed number of elements on AB, CD and DA edges 

  • Imposed middle point for triangle mesh

See the values in the table of results.

Restraints (User-defined):

  • At point A: Tz=0

  • On edge AB: Ty=Rx=Rz=0

  • On edge CD: Tx=Ry=Rz=0

Loads (Distributed force):

F=1 (outward at A, inward at D)
 

Results

  • The analytical solution is:
    At point A, x-displacement is 94 mm.

  • The results correspond to the x-displacements at point A.
    The table below presents the analysis results.
    The normalized results (computed results divided by analytical solution) are listed.
     

 Nodes  

Values

Linear
triangle (TR3)

Parabolic
triangle (TR6)

Linear
quadrangle (QD4)

Parabolic
quadrangle (QD8)

Computed results
[mm]

Normalized results

Computed results
[mm]

Normalized results

Computed results
[mm]

Normalized results

Computed results
[mm]

Normalized results

3 x 3

105.9

1.127

95.33

1.014

71.17

0.757

21.82

0.232

5 x 5

98.19

1.045

91.68

0.975

95.76

1.019

77.12

0.820

7 x 7

96.36

1.025

94.06

1.001

96.39

1.025

93.00

0.989

9 x 9

95.53

1.016

93.55

0.995

95.38

1.015

94.36

1.004

11 x 11

96.50

1.027

93.87

0.999

94.89

1.009

93.72

0.997

13 x 13

93.15

0.991

93.21

0.992

93.97

0.999

93.04

0.989

To Perform the Test:

The hemispherical_shell_concentrated_loads_13nodes_tr6.CATAnalysis document presents a complete analysis of this case, computed with a mesh formed of parabolic triangle elements (TR6).

The hemispherical_shell_concentrated_loads_13nodes_qd8.CATAnalysis document presents a complete analysis of this case, computed with a mesh formed of parabolic quadrangle elements (QD8).

To compute the case with other types of elements and number of nodes, proceed as follow:

  1. Open one of the CATAnalysis documents.

  2. Enter the Advanced Meshing Tools workbench.

  3. In the specification tree, double-click on the mesh.

    The Global Parameters dialog box appears.

  4. Select the Linear element type.

  5. Compute the case in the Generative Structural Analysis workbench.