Composites Fiber Modeling can be used successfully with the same input parameters as the standard fiber simulation tool in Producibility.
However, to make full use of Composites Fiber Modeling capabilities, additional data can be provided to obtain a more accurate simulation result. The additional data include:
- Definition of a seed curve to constrain the fiber simulation along a curve.
- Definition of one or more order of drape regions by means of contours on the surface of the ply.
- Selection of advanced propagation types to reflect the behavior of materials according to the manufacturing processes.
- Preview of the flat pattern to provide excellent feedback on the fiber simulation.
With the enhanced Producibility dialog box, Composites Fiber Modeling allows you to define specific parameters and store these in Producibility params.x under each ply. Those parameters may be:
- Simulation: Advanced parameters. They affect the actual fiber simulation,
- or Analysis: Advanced parameters. They affect the display of the fiber simulation results, are used for additional display options provided by the solvers, which are added to the Deformation list.
Seed Point
The seed point is defined in same way as for the standard fiber simulation. However, Composites Fiber Modeling supports seed points located on the boundary of the ply. This reflects the normal practice where the application of the ply often begins along the edge of the region to be covered.
In general, the material is unsheared at the seed point and shearing increases away from that point. The amount of shear in a ply made of a particular material increases with distance from the ply, and the degree of Gaussian curvature of the surface (this is a reflection of the double-curved nature of the surface, when applicable). Therefore, to minimize shear, the seed point should be located:
- To minimize the distance to any part of the ply boundary - so the middle would reduce shear, at the cost of being impractical.
- To minimize the Gaussian curvature near the start point. In fact, it is a good idea to begin draping on a region of near-zero Gaussian curvature if this is possible.
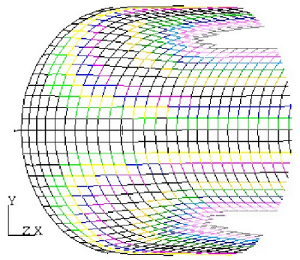
As an example, consider half of a pressure vessel which consists of a
spherical cap with a cylindrical body. If the seed point is on the
cylindrical body, which has zero Gaussian curvature and is furthermore
developable, limited shearing only occurs over the spherical section.
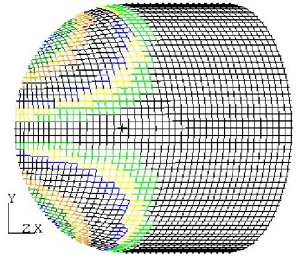
By contrast, if the seed point is on the spherical section, shear builds
up rapidly and the surface cannot even be covered.
Seed Curve
A seed curve forces the warp, weft or bias directions of the fabric along
a curve. The curve must pass through the seed point, and must extend to the
ply boundaries. In the following example, the bias direction of the fabric
has been forced along a curve through the middle of the spar. This results
in a flat pattern with parallel sides, which is a tape.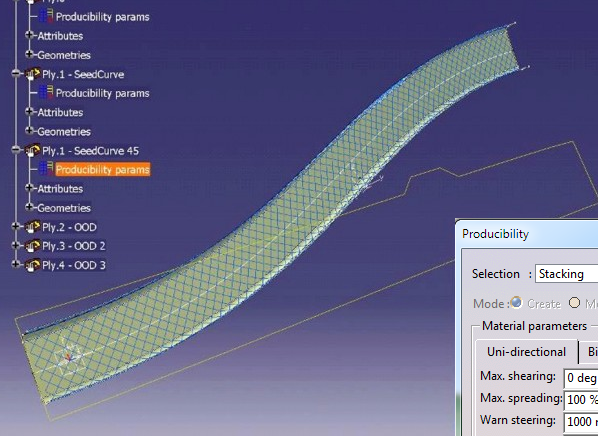
The choice of whether the warp, weft or bias directions are forced along the curve depends on the relative alignment of the nominal warp and weft directions at the seed point, and the seed curve at this point.
The woven construction of the fabric is defined by physical
parameters that reflect the structure of the material.
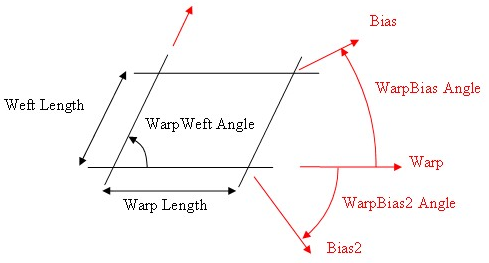
In Composites Fiber Modeling, the Warp/Weft angle is defined under Simulation: Advanced parameters, and information is found under Material parameters, while the Warp and Weft length ratio is set under the Mesh parameters. For the purposes of defining the unit cell, it is the ratio of warp and weft lengths that is important. So, if warp and weft lengths are the same, the bias directions are at +/- 45 degrees.
The axis forced along the seed curve is the closest to the seed curve at the seed point. For example, if the Warp/Weft angle is 90 degrees and the warp and weft lengths are identical, and if the seed curve lies 30 degrees from the nominal warp direction, the bias direction is closest to the seed curve and this is the direction forced along the seed curve.
This snapping to the nearest direction means that the actual and nominal warp directions at the seed point may be slightly different - 15 degrees in the case above. This must be accounted for when using the inspection tool.
The seed point must be located on the seed curve, otherwise an error message is displayed. In practice, a tolerance of 1% of the square root of the ply area is allowed to permit small separations between seed point and seed curve resulting from the Thickness Update capability, for example.
Order of Drape
The order of drape capability allows you to model the exact sequence used to apply fabric to surfaces on the shop floor. The order of drape regions define smaller surfaces that are covered in one sequence, and which provide a stable initial condition for subsequent application of material.
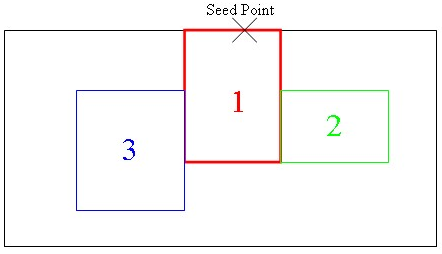
In the example below, we have defined three order of drape regions:
- The first order of drape region marked in red (1) must contain the seed point, otherwise it is ignored.
- At the end of the first sequence, the area defined by the second order of drape region marked in green (2) is covered by fabric using the first order of drape as a starting point.
- The third order of drape region (3) is similarly covered next.
- Finally, all the remaining area of the ply is covered.
We do not recommend to have too many order of drape regions on a single ply. Usually, between one and two regions are sufficient.
It is a good idea to define order of drape regions on relatively flat regions of the surface. This means that the position of the seed point is not significant, and this lack of sensitivity follows through the simulation, resulting in a robust final result, that will be easily manufacturable.
In general, it is best if the summed boundaries of all the order of drape
regions are straight or convex. If they are concave with respect to a warp
or weft fiber, the fiber in the fabric might be
over-constrained as shown below.
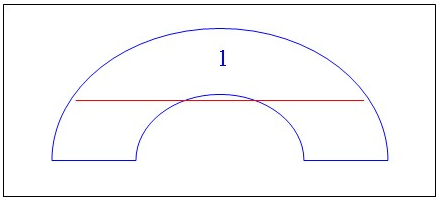
Here, the first order of drape region will drape perfectly well with its shape. But consider the red fiber as the drape extends beyond the first region. Here, the fiber suddenly becomes over-constrained as the drape extends across the concave boundary, so that the fibers become kinematically inadmissible.
To handle this situation, Composites Fiber Modeling will, by default, unstick fabric on one branch of the semi-circle (keeping the branch where the red line is longest) to remove the excessive constraint. This behavior is followed if the Inadmissible Mode is set to Delete, i.e. the constraint is deleted as necessary. Note that the flat pattern over the order of drape region can change in subsequent drapes.
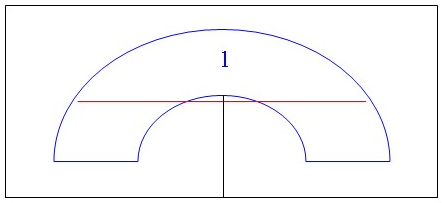
This situation of kinematic inadmissiblity can be resolved easily by
simply placing a dart in the middle of the semi-circular region using the
limit contour capability as shown below. This dart removes the excessive
constraint and allows draping to proceed.
You can force Composites Fiber Modeling to keep the fabric stuck to the order of drape regions during subsequent extensions if Inadmissible Mode is set to Cut. In this case, kinematically inadmissible fibers are avoided by automatically generating a rough cut in the middle of a bounded length in an over-constrained fiber, such as that shown in red in the figure above. This cut will only be created if the strain required in the fiber to allow it to conform to the surface exceeds the inadmissible tolerance value set, or the displacement mismatch at the cut location exceeds half a step length in the appropriate direction. This approach has the advantage of keeping the flat pattern in an order of drape region constant during subsequent draping, but forces you to define a dart to specify the flat pattern shape around the dart accurately. This methodology is recommended for highest accuracy on components like curved frames where it is impossible to avoid concave order of drape boundaries.
Seed curve and order of drape can be combined if required, but the seed curve (and seed point) should lie in the first order of drape region.
Smooth Regions
A smooth region is an area where the simulation can ignore awkward bumps/hollows for an initial global simulation. The subsequent local draping goes from the smooth region boundary towards the middle of the bumps/hollows
Many composite structures contain "bumps" - a ubiquitous example
is that of a sandwich panel incorporating cores. When laying plies
over the bumps, the material necessarily shears to conform
to the highly-curved surface covering the bumps. This shearing
deformation is indicated by the red fibers on the J-panel
below.
However, it is often necessary to define plies that lie around the bumps, but do not cover them. As most fiber simulations cannot accept holes in the surface used for simulation, the underlying surface that includes the bumps is used for the simulation, so high shear is still predicted whereas the surface excluding bumps may be rather simple and not need excessive shear.
Draping result with smooth regions
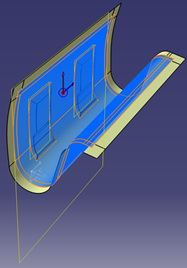
The smooth region is defined by an area and a curve.
- The area, with or without an order of drape, specifies a developable region.
- The smooth region curve defines a bump inside to be filled with a smooth surface using point, tangent or curvature.
In the image below:
- 1 represents the bump.
- 2 represents the manual trimming area.
- 3 represents the smooth region boundary.
- 4 represents the required dart.
- 5 represents the finished inner boundary.
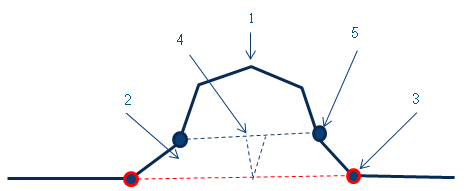
The example below has an interior contour. Without a smooth region, draping occurs over the entire surface causing strain to be distributed in places where it is undesirable. With a smooth region curve:
- The smooth region is filled with a surface and combined with the ply shell.
- This new smooth surface is simulated to create a low strain surface giving good edges.
- Next, the area inside the smooth region curve is added, and any strain is propagated into this region. Generally, causing the need for darts.
- The blue arrows shows the interior contour, the pink arrow shows the smooth region curve.
- This is the difference of flat patterns.
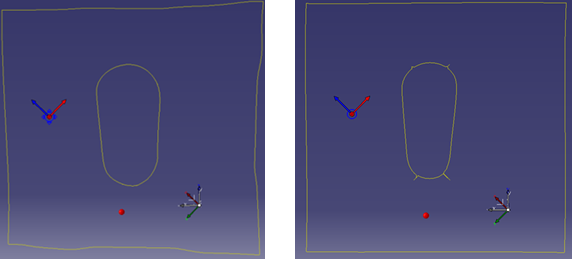
The smooth region boundaries should not cross ply boundaries (possibly modified by darts) nor order of drape region boundaries. If an inner ply boundary lies inside a smooth region boundary, dart the material at the inner boundary. If you do not define darts, the simulation proposes rough darts as the models for the darts to define. The inner darts should extend to the smooth region, but not cross it.
Mesh Parameters
The Mesh parameters define the architecture of the fabric, and the step lengths used for the fiber simulation.
Regarding the architecture of the fabric, the ratio between warp and weft is constant for a particular material and this material property should be used consistently. This is especially important when using a seed curve.
The fiber simulation in Composites Fiber Modeling is relatively insensitive to step length. This makes the simulation accurate for highly curved surfaces, and reduces sensitivity to step length.
Consider the following channel section. For a wide variety of step
lengths (between 1 and 50 mm), the Composites Fiber Modeling result
predicted the same flat pattern. By contrast, the standard fiber simulation
gave very different results depending on the chosen step length, and large
step lengths lead to very poor flat pattern results.
As a result of the insensitivity to step length, there is no need to have very small step lengths and this can, in fact, be counter-productive.
Fine detail on the edge of the ply is picked up irrespective of the step length.
As can be seen in this screen-shot,
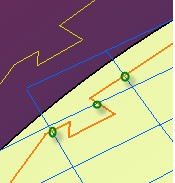
the warp and weft lines (blue) at the spacing requested by the user have
crossed the line defining the ply boundary (orange) at the location marked
with circles (green).
The line showing the flat pattern (yellow) still contains the fine detail of the edge, which will reflect the local strain in the ply.
There is no need to set a small spacing to pick up details
Please note that the fiber VISUALISATION in the Composites Workbench does not reflect the fact that the underlying simulation in Composites Fiber Modeling follows the underlying surface exactly. However, this is simply a property of the Composites Workbench and does not reflect the accuracy of the results.
Propagation Type
The propagation type reflects the way in which the fabric covers the surface. As a consequence, different propagation types lead to different shapes and measures for the flattened ply.
Consider fabric placed on a surface beginning at the seed point
with the principal warp and weft fibers defining seed curves being shown in
red below. If the red lines are constrained to the surface, the placement of
the fabric bounded by the green line is then uniquely defined.
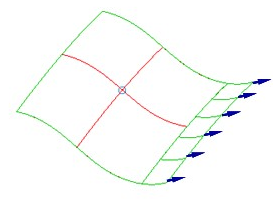
Extending the material further to the ply boundary is done one free edge at a time. When extending a free edge, the fabric behaves as a trellis and so the exact direction of growth is not fully defined. Therefore, assumptions must be made of the direction of growth based on the material behavior and manufacturing method. Composites Fiber Modeling provides several different propagation modes to cover the most important manufacturing options, that fall into three categories.
- Optimized Energy and Optimized Maxshear modes use a biaxial material model and a circular extension strategy to model the hand layup of woven fabrics.
- Second, the Tape and UD Tape modes use a strip extension strategy to simulate the application of biaxial or uniaxial tape respectively in a way which accurately reflects the real-world application of butted tapes of material onto a surface by manual means. This is also likely to reflect butted tape laying via automated means, subject to the fact that the detailed characteristics of the tape laying machine are not known by Composites Fiber Modeling.
- Finally, the FEFlatten propagation mode predicts the flattening of plies using finite element analysis techniques and is applicable to fabrics without a biaxial or uniaxial microstructure.
Circular Propagation Modes
In the circular extension modes (Optimized Energy and Optimized Maxshear), free edges in the warp and weft directions are extended alternately so that the ply extends uniformly in all directions away from the seed point. This models the operator progressively smoothing the fabric onto the mould away from the seed point.
- Propagation with circular strategy: alternate warp and
weft extension:
The two options reflect different shear load deflection-behavior of the
ply material. The best indicator of behavior is a graph of the shear
stress/strain response of the material. Typical stress-strain curves are
shown below.
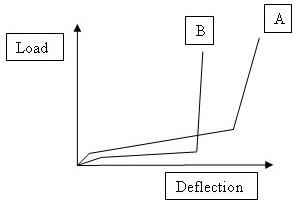
Typically, after a small elastic range, the material begins to shear significantly with little resistance. This continues up until the warp and weft fibers begin to lock, and stiffness increases rapidly. The range of behaviors is wide and depends on the weave architecture, presence of binder, and many other factors.
- In general, Optimized Energy propagation type that seeks to minimize the shear strain energy on an extending (propagating) edge gives excellent results for a wide variety of fabrics.
- On the other hand, if locking occurs suddenly in the fabric (as in curve B above), it is better to limit the maximum shear as much as possible. In this case, the Optimized Maxshear propagation mode is more suitable.
- Whatever propagation mode, excellent results should be obtained as long as the material is cut to a net shape, the seed point is accurately located, and the material is applied with due reference to the ply edge.
A sample drape using a circular propagation mode is shown below. The area of least shear spreads away from the start point along the
principal axes. The amount of shear is minimized by the algorithm actively
working to limit the shear, as a skilled operator would do.
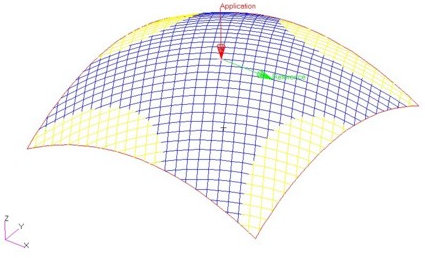
Geodesic propagation mode extends principal geodesic lines from the Seed Point to the ply boundary (or the boundary of the first order-of-drape region, if smaller) in the initial directions of warp and weft yarns. This uniquely constrains the fabric bounded by the principal fibers. If draping continues beyond this region, geodesic fibers are extended as required in warp and weft directions from points closest to the principal fibers until the surface is covered.
This propagation type gives good results on surfaces of low curvature, but can lead to excessive shear for regions of high curvature.
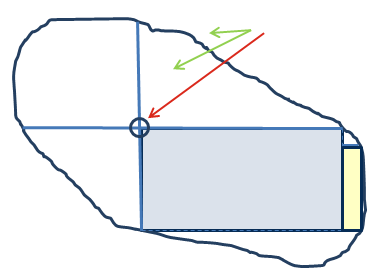
In the image below
- The green arrows point to the seed points.
- The red arrow points to principal fiber along geodesic path.
- The blue rectangle represents the constrained region, the yellow one the extension nearest principal fiber.
Energy (Frictionless): In general, simulations of hand layup assume that the fabric sticks to the surface completely as soon as it is smoothed onto the surface. This is an appropriate assumption for most hand layup materials and processes, but has the effect of locking in excessive material deformation.
Energy (Frictionless) propagation mode models the case of no friction between fabric and mold. It allows the fabric to move to minimize the overall shear strain energy in the material. This yields a unique solution for a particular Seed Point (which should instead be considered as a Reference Point) and initial warp direction and indicates idealized fiber paths that minimize overall ply deformation. Also to be used to estimate deformation during matched die forming. Energy (Frictionless) is intended to model forming between two frictionless forms, and uses an iterative solution to minimize the shear strain energy throughout the ply. This means that the material may shear at the indicated point, which is a Reference Point and not a Seed Point. The solution should not be highly dependent on the location of the Reference Point, but computationally the best location for this point is near the center of the ply - so the Geometrical Center option is suggested as a starting point.
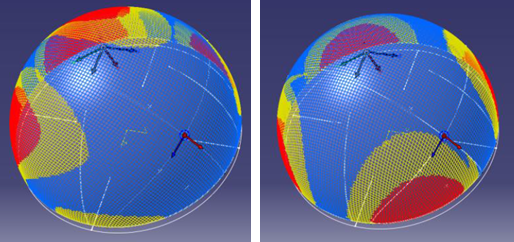
A comparison between results from the Optimized Energy (on the left) and
Energy (Frictionless) (on the right) propagation modes for a non-symmetrical
seed/reference point is shown below. As you can see, Energy
(Frictionless) acts to reduce shear despite the reference
point not being in the middle of the ply.
Energy (Frictionless) runs an initial Optimized Energy solution and then iterates the results to minimize shear strain energy. The solution is therefore an order of magnitude slower and can be less stable than standard results.
Strip Propagation Modes
In the strip extension modes (Tape and UD Tape):
- the first tape is extended from the seed point in the warp direction all the way to the ply boundary in both the positive and negative warp directions.
- Only once this first tape is laid are additional tapes abutted against the free weft edges of the preceding tapes.
- For each new tape, the material
strain is set to zero at the point of first application, which is defined as
the point in the most negative warp direction. This reflects the fact that
the material is unsheared at the point of first application on a surface.
The rate of increase of shear along the tape depends on the width of the
tape and the Gaussian curvature of the surface.
- Propagation with strip strategy: initial warp extension,
then lateral weft
- Propagation with strip strategy: initial warp extension,
then lateral weft
Both tape propagation modes use the same extension type but differ slightly in the material model used.
- The Tape mode uses a standard biaxial
material model where it is assumed that warp and weft fibers
pivot about their cross-over points so that an
initially-square piece of material becomes a rhombus after
shearing in a scissor mode as shown below.
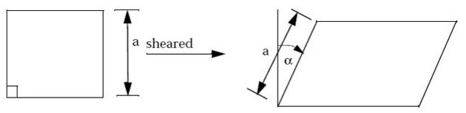
Importantly, the lengths of the sides remain constant as they are sheared. - Alternatively, for uniaxial materials modeled by the
UD Tape option, parallel fibers are assumed to
remain parallel and equidistant, with shearing resulting
from the relative sliding of fibers.
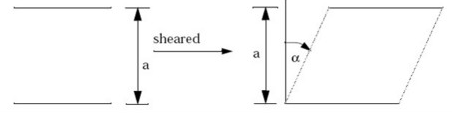
In practice, the results of the two material models converge on the same solution for small shears. At higher shears, the warp fibers of a biaxial material close up, which tends to reduce the amount of shear in a ply covering a surface of positive Gaussian curvature. In general, the Tape option will be more robust than the UD Tape option.
A sample drape using the Tape propagation model is shown
below.
Note that:
- the shear is zero along the principal warp direction as in this case, this follows a geodesic line on the surface.
- the shear is zero by definition at the minimum warp end of each tape.
- the degree of shear is higher than for the circular algorithm above.
FEFlatten Propagation Mode
The circular and tape propagation modes mentioned previously are based on a geometrical fiber simulation and give excellent results for Uniaxial and Biaxial materials where the material deforms in a highly directional way with almost no deformation along the fibers and concentrated deformation between fibers.
However, some materials used for Composites parts behave in a more isotropic manner with the material deforming in a direction imposed by the applied force and tractions within the ply rather than forced in a particular direction due to the underlying fiber architecture.
These include the following sheet materials commonly used in the manufacture of laminated structures:
- Quadraxial Non-Crimp Fabrics (NCF)
- Chopped Strand Mat (CSM)
- Knitted Fabrics
- Foam Cores
- Vinyl and Leather
In order to calculate the flat and draped patterns of these materials, a purely geometrical approach cannot identify the important load paths in the fabric as it is forced over a doubly-curved surface and instead a finite-element based flattening (FEFlatten) solution is required.
The finite element flattening approach:
- effectively calculates the initial flat shape of the ply assuming that the material is formed between two frictionless dies. This allows the calculation of a smoothed minimum energy solution over the whole ply. The solution is a sophisticated extension of the approach of McCartney et al (1999, 2005) coupled with the use of nonlinear finite element analysis techniques.
- The solution time can be expected to be of the order of minutes.
- This technique can be thought of as lying between a purely geometrical simulation, taking seconds, and a full-contact multi-ply finite element calculation, taking days.
- A particular advantage of the FEFlatten solution is that interior holes can be free boundaries, so that surfaces containing holes (or bumps/hollows surrounded by interior contours) can be solved without problems.
- A comparison between geometrical fiber simulation and finite element flattening approaches is given in the table below:
| Geometrical Fiber Simulation | Finite Element Flattening |
| Initial value problem, local energy minimization | Boundary value problem, global energy minimization |
| Exact flatten around details | Flatten smeared by finite element definition |
| Solution in seconds | Solution in minutes |
| Holes cannot be free boundaries | Holes can be free boundaries |
| Uniaxial, Biaxial materials | Isotropic, general materials |
A comparison of simulation results obtained through the standard Composites Fiber Modeling geometrical solvers, and the Composites Fiber Modeling flattening solver, for a mesa-like protuberance on a gently curved surface is given below. This clearly shows that by allowing strain along the fibers, the FEFlatten propagation mode reflects the reduction of peak strains in the material.
| Geometrical Fiber Simulation | Finite Element Flattening |
| Pin Jointed Net | Finite Elements |
| Pure Shear Strain | Shear + Normal Strain |
| Concentrated Deformation | Distributed Deformation |
 |
 |
 |
 |
Display Modes
The 3D draped pattern for Composites Fiber Modeling is displayed in the same way as the standard fiber simulation. This means that the result can be used for inspection and 2D-3D transfer, and can be stored as curves in the V5 part.
Note that the graphics visualization provided by CATIA does NOT reflect the underlying simulation completely in the following respects:
- Composites Fiber Modeling follows the surface EXACTLY, while the visualization only joins points on the surface
- Composites Fiber Modeling continues the simulation to the edge of the ply, whereas the CATIA visualization does not allow the display of partial fibers and so the "Lonely Points" are removed.
When using the enhanced producibility panel in CATIA V5R19 onwards, users can access specialized display modes relevant to the fiber simulation. These give additional insight into the deformation of the ply over and above the degree of pure shear visualised in the standard Shearing Angle display mode. Composites Fiber Modeling currently supports display of the Steering Radius (not FEFlatten), and Axial Strain (only FEFlatten solver).
Steering Radius (not FEFlatten)
The steering radius is the radius of curvature of the fibers in the plane of the surface. This information is particularly useful for investigating the viability of tape laying, where the forming limits of tape are usually characterized by the minimum manufacturable radius of curvature.
The steering radius is also an additional measure of the degree of deformation in fabrics and can complement the standard shearing angle display.
Axial Strain (only FEFlatten)
The FEFlatten solver admits the possibility of axial strain along the nominal warp and weft fibers. It is only valid for the FEFlatten solver as the value would be zero for other solvers.
Maximum Slope
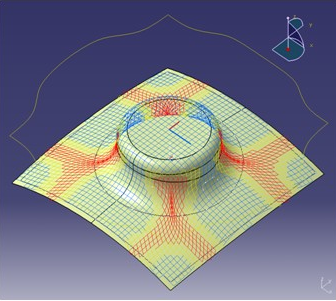
Thickness Update provides a powerful capability to offset the simulation mesh from the ply definition surface. The result is a very accurate flat patterns of plies offset from the mold surface (far better than offsetting by a constant thickness). However, for complex layups, there are situations where the resultant updated surface becomes uneven.
As an example, consider the case of a two plies that are separated by a small gap (This may be intended by the designer to promote resin flow). 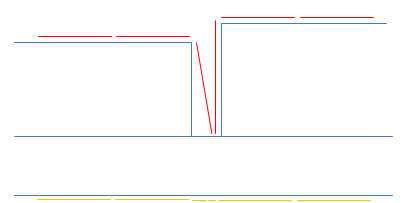
Here, the surface simulation mesh (in yellow at the bottom) is necessarily defined to respect ply boundaries on the surface, but when updated, results in a surface (in red on top).
Since
Composites Fiber Modeling produces very accurate flat patterns as it follows the surface absolutely, it is disproportionately affected by surface quality. In fact, the surface roughness described above is seamlessly handled by Composites Fiber Modeling, but the effect of generalized crossing of hundreds of ply boundaries can be unpredictable. To solve this problem while taking advantage of the power of Thickness Update, smooth the simulation surface by choosing a maximum slope of the offset facets measured from their baseline position as shown below. 
This effectively removes simulation surface artifacts and results in stable simulations with better results.
Display Flat Pattern
Composites Fiber Modeling computes the flat pattern instantaneously as an intrinsic feature of its simulation, thus ensuring:
- Accuracy, as it is an intrinsic part of the simulation process,
- Speed, as no separate process is involved,
- Clarity, as it is possible to visualize the 2D flat pattern at the same time as the 3D draped pattern.
To display the flat pattern at the same time as the draped pattern, simply check the "Display Flat Pattern" box. The flat pattern will then be displayed in a plane parallel to the surface at the seed point, and with the correct orientation.
The feedback allowed by this feature gives the user immediate
confidence in the quality of the fiber simulation. 
![]()