Breaking Elements

Applying the Break command to intersecting lines creates a point at the geometry intersection.

This task shows how to break a line that does not intersect geometry, in different ways:

Break lets you break any type of curve, except for composite curves. You can use any Sketcher element to break curves.

Create two lines and a point and ensure that the Geometrical Constraints is activated .

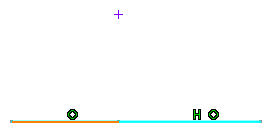
Use a Point on the Line
 

  1. Click Break in the Operation toolbar (Relimitations sub-toolbar).

  2. Select the line to be broken.
    The start point and the probable break point are displayed immediately. The break point changes as you move the pointer over the line.

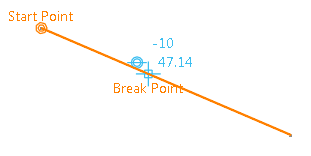
  3. Indicate where to create the break.

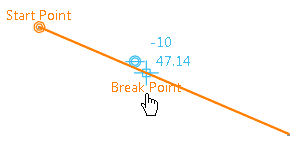
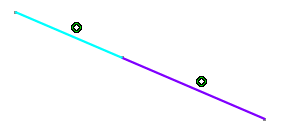
    The line is broken at the indicated point. The broken entity is highlighted and a point is created. The line is now composed of two segments. Coincidence constraints are created and represented by two small concentric circles.
 

Use a Point Belonging to Another Line
  You can break a line at a point using a point on another line. For this you need to select the line and indicate on the other line where to break the selected line. The line is broken from the projection of the selected point and it also considers the possible constraints associated with the two elements.
 

  1. Click Break .

  2. Select the line to be broken.
    The start point and the probable break point are displayed immediately.

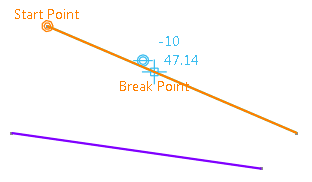
  3. Select the second line.
    The projection of the selected line is displayed along with the possible constraint.
     

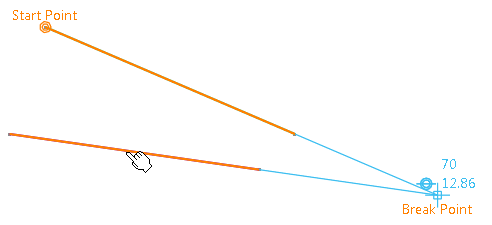
    The line is broken from the projection of the selected line which intersects the projection of the first line considering the possible constraint.
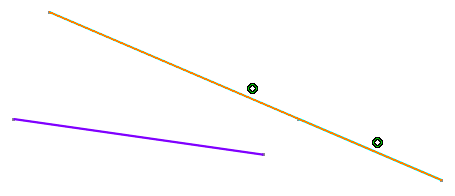
    Hold down Shift while selecting the second line if you do not want to consider the possible constraints. In this case, the line is broken from the projection of the selected point: a projection point of the selected point is created.

    The line is now composed of two segments. Coincidence constraints are created.
 

Use a Point
  To break a line at point, select a line and a point. The line is broken from the projection of the selected point: a projection point of the selected point is created. The line is now composed of two segments. Coincidence constraint is created.

  1. Click Break .

  2. Select the line to be broken.

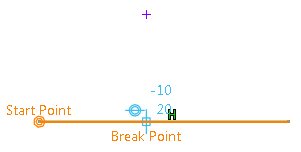
  3. Select the breaking point.
    The projection of the point is automatically displayed.

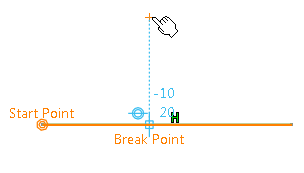
    The line is broken from the projection of the selected point: a projection point of the selected point is created. The line is now composed of two segments. Coincidence constraints are created.
 

More about the Break Command

Using the Break , you can also isolate points:

  • if you select a point that limits and is common to two elements, the point will be duplicated.
  • if you select a coincident point, this point becomes independent (it is no more assigned a coincidence constraint).
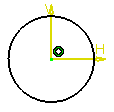
    In the following example, applying  Break onto the circle center lets you therefore move the circle:
           
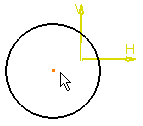
  • You can isolate a point by right clicking the point and selecting Point.x object > Isolate Point(s) after you apply Break.
    A new separate feature Point.x is added to the specification tree for the isolated point, isolated using the Isolate Point(s) command.

     
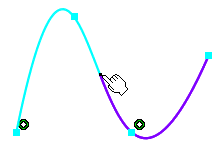
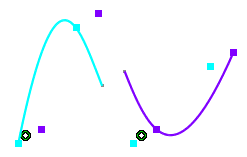
  • If you move the pointer over different entities when using the Break command, the point's representation is also updated that is the start point and the break point.
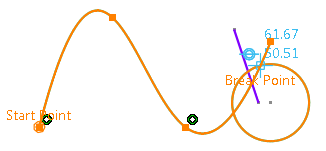
  • The different parts of the curve get highlighted when you sequentially move the pointer over different elements when selecting the breaking element. Thus the highlighted elements are changed whenever the entity under the pointer changes while selecting the breaking element.

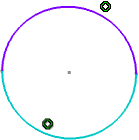
    If you select a circle as a breaking element, the start point is indicated across the horizontal axis as shown below:

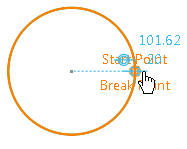
    The break point changes as you move the pointer over the circle.



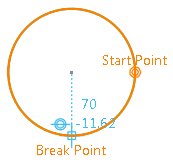
    After applying break, the circle is broken at the indicated point. The broken entity is highlighted and a point is created. The circle is now composed of two segments. Coincidence constraints are created and represented by two small concentric circles.

Composite Curves

You cannot break composite curves (which are projected/intersected elements composed of several curves). However, you can work around this functional restriction by projecting or intersecting the composite curve elements and break these items using one another.